The term typical deviation or standard deviation refers to a measure used to quantify the variation or dispersion of numerical data in a random variable, statistical population, data set, or probability distribution.
The world of research and statistics may seem complex and foreign to the general population, since it seems that mathematical calculations happen under our gaze without us being able to understand their underlying mechanisms. Nothing is further from reality.
On this occasion we are going to relate in a simple but at the same time exhaustive way the context, the foundation and the application of a term as essential as the standard deviation in the field of statistics.
What is the standard deviation?
Statistics is a branch of mathematics that is responsible for recording variability, as well as the random process that generates it. following the laws of probability This is said quickly, but within statistical processes are the answers to everything that we today consider as “dogmas” in the world of nature and physics.
For example, let’s say that when you toss a coin three times in the air, two of them come up heads and one tails. Simple coincidence, right? On the other hand, if we toss the same coin into the air 700 times and 660 of them land on heads, perhaps it is possible that there is a factor that causes this phenomenon beyond randomness (let’s imagine, for example, that it only has time to give a limited number of turns in the air, which means that it almost always falls in the same way). Thus, the observation of patterns beyond mere coincidence prompts us to think about the underlying reasons for the trend.
What we want to show with this bizarre example is that Statistics is an essential tool for any scientific process because based on it we are able to distinguish realities resulting from chance from events governed by natural laws.
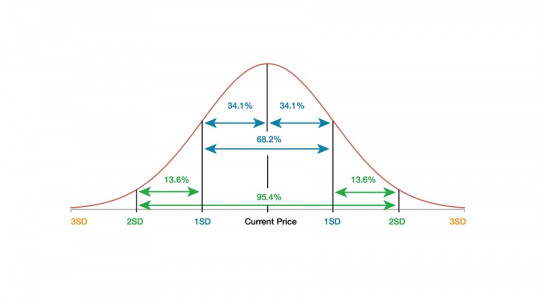
Thus, we can throw a hasty definition of the standard deviation and say that it is a statistical measure product of the square root of its variance. This is like starting the house with the roof, because for a person who is not entirely dedicated to the world of numbers, this definition and not knowing anything about the term are little different. Let us then take a moment to dissect the world of basic statistical patterns
Measurements of position and variability
Position measures are indicators used to indicate what percentage of data within a frequency distribution exceeds these expressions, whose value represents the value of the data that is in the center of the frequency distribution Do not despair, because we define them quickly:
In a rudimentary way, we could say that position measures are focused on dividing the data set into equal percentage parts, that is, “getting to the middle.”
On the other hand, variability measures are responsible for determine the degree of approach or distance of the values of a distribution compared to their location average (i.e. compared to the average). These are the following:
Of course, we are moving in relatively complex terms for someone who is not entirely dedicated to the world of mathematics. We do not want to go into other measures of variability, since knowing that the greater the numerical products of these parameters, the less homogenized the data set will be.
“The average of the atypical”
Once we have cemented our knowledge of variability measures and their importance in data analysis, it is time to refocus our attention on the standard deviation.
Without going into complex concepts (and perhaps erring on the side of oversimplifying things), we can say that This measure is the product of calculating the average of the “atypical” values Let’s take an example to clarify this definition:
We have a sample of six pregnant dogs of the same breed and age who have just given birth to their litters of puppies simultaneously. Three of them have given birth to 2 puppies each, while three others have given birth to 4 puppies per female. Naturally, the average value of offspring is 3 puppies per female (the sum of all puppies divided by the total number of females).
What would be the standard deviation in this example? First of all, we would have to subtract the average from the values obtained and square this figure (since we do not want negative numbers), for example: 4-3=1 or 2-3= (-1, squared, 1) .
The variance would be calculated as the average of the deviations from the mean value (in this case, 3). Here we would be dealing with the variance, and therefore, we must take the square root of this value to transform it into the same numerical scale as the mean. After this we would obtain the standard deviation.
So what would be the standard deviation for our example? Well, a puppy. It is estimated that the average litter size is three offspring, but it is normal for the mother to give birth to one less puppy or one more per litter.
Perhaps this example could sound a little confusing as far as variance and deviation are concerned (since the square root of 1 is 1), but if in it the variance were 4, the result of the standard deviation would be 2 (remember , its square root).
What we wanted to show with this example is that Variance and standard deviation are statistical measures that seek to obtain the average of values other than the average Let us remember: the larger the standard deviation, the greater the dispersion of the population.
Returning to the previous example, if all the dogs are of the same breed and have similar weights, it is normal for the deviation to be one puppy per litter. But for example, if we take a mouse and an elephant, it is clear that the deviation in terms of the number of offspring would reach values much greater than one. Again, the less the two sample groups have in common, the greater the deviations will be expected.
Still, one thing is clear: using this parameter we are calculating the variance in the data of a sample, but this does not have to be representative of an entire population. In this example we have caught six dogs, but what if we monitored seven and the seventh had a litter of 9 puppies?
Of course, the pattern of deviation would change. For this reason, take into account Sample size is essential when interpreting any data set The more individual numbers are collected and the more times an experiment is repeated, the closer we will come to postulating a general truth.
Conclusions
As we have seen, the standard deviation is a measure of data dispersion. The greater the dispersion, the greater this value will be since if we were faced with a set of completely homogeneous results (that is, they were all equal to the mean), this parameter would be equal to 0.
This value is of enormous importance in statistics, since not everything is reduced to finding common bridges between figures and events, but it is also essential to record the variability between sample groups in order to be able to ask more questions and obtain more knowledge in the long term.